Gunosyのパーソナライズを支える技術 -計算モデルとアーキテクチャ編-

この記事は Gunosy Advent Calendar 2017 の1日目の記事です(フライング)

qiita.com

§1. はじめに

こんにちは。データ分析部ロジックチームの @mathetakeです。いつもはデータ分析ブログにいるのでテックブログは初めてです。怖いです。Twitterとかやったことないですね。

最近は仕事でニュースパスというプロダクトの記事配信ロジックの改善を行っており、その一環としてパーソナライズロジックの開発プロジェクトに従事しています。

パーソナライズとはユーザーひとりひとりに対して別々の記事配信を行う事です。下記の記事でパーソナライズプロジェクト発足に至るまでの背景が語られているので、興味のある方はぜひご覧ください。

gunosiru.gunosy.co.jp

この記事ではニュースパスの記事配信アルゴリズムのパーソナライズプロジェクトに関連して、

パーソナライズの背景
アーキテクチャ概説
記事スコア*1計算モデルの概要
パーソナライズされた記事リストを返すAPIサーバーの処理

について書きます。ほぼ毎月行われているGunosy Tech Night*2での発表内容を元にしています:

§2. 背景とマイルストーン

パーソナライズpjの背景は、上記の記事の内容(+α)をざっとまとめてみると

バッチ処理でユーザー属性の数だけリストを事前に生成することの限界
- 興味関心の取りこぼしが生まれる
- 組み合わせの数だけ処理が必要になりスケールしない

技術的負債
- 最重要である記事配信ロジックの改善のサイクルが回しづらい
- カジュアルにロジックのABテストが行えない
- 複雑に入り組んだコードになっているため新しいメンバーのキャッチアップが大変

こんな感じです。

このような背景があり、パーソナライズプロジェクトの最初のマイルストーンとして例えば

ユーザーのリクエストトリガーで記事リストをリアルタイムに生成する
リアルタイムにユーザーの興味嗜好の変化を反映する仕組みの導入
既存の記事生成の仕組みを使わずゼロから作り直す

を設定しました。

§3. アーキテクチャ

まずパーソナライズシステム全体のアーキテクチャについて簡単に説明します。
大人の事情により勝手にマル秘と表示されている箇所があります。困った困った。

ざっくりまとめると

後述の計算モデルに必要なものは全てDynamoDBとs3におく
関連するほぼすべてのタスクのワークフローはdigdagにより管理
例外はリアルタイム性を求められるユーザーベクトルを生成するAWS lambda

こんな感じです。digadagの運用とリアルタイムベクトル生成AWS lambdaについては後日別記事で解説します。

開発言語ですが

Spark on EMRクラスタを用いてマル秘機械学習を行っている部分はScala
パーソナライズド記事リスト返す記事APIはgolang
その他タスクは基本的にpython

と言った感じです。

クライアントからのリクエストは必ず一番右にある Gateway API を介し、ABテストのために複数存在する記事APIのうち、どのエンドポイントを叩くかを制御しています。これにより無駄なifを書くことなく、つまりソースコードを汚すことなくABテストを行うことが可能となっています。幸せですね。

以降の§では、記事APIがどのような計算モデルによって記事をスコアリングし、リストを生成するかについて述べていきます。

§4. スコア計算モデルとハイパーパラメータ

まず最初に、スコア, スコア計算モデルという言葉の定義をはっきりさせておきます。

スコアとは記事を出すべきかを表す数値のことです。候補となる記事全てに対してスコアを計算し、それを元にソートしてからユーザーに表示するというのが基本的なアルゴリズムになります。

スコア計算モデルとは、ユーザー $u$ と記事 $a$ を引数にしてスコアを算出する時間によって変化する関数 $s_t$

${s_t: \{ ユーザー \} \times \{ {\rm ニュース記事} \} \rightarrow \mathbb{R} , \ \ \ (u, a) \mapsto s_t(u,a) , \ \ t: 時間 }$

のことです。我々の目標はより"良い" $s_t$ を構築する事ですが、その制約条件として

リアルタイムに数千からなる候補記事全てに対するスコア計算を行う

があります。

そこで今回ver.1として、少しふわっとしてますが

記事APIが行う計算部分は行列演算のみで済む線形モデル
線形モデルの各項に非線形な効果が入るように非同期なタスクを裏側で走らせておく

このようなスコア計算モデルを設計しました。

これにより、記事APIが行う処理は行列演算のみなので現実的な時間内にレスポンスすることが可能になり、かつ非線形な効果も入るのでそこそこ良いモデルになっています。

より詳細に(と言ってもマル秘を含みますが)解説するために、まず線形モデルに組み込まれるユーザーの特徴量が生成されるまでの流れを説明します:

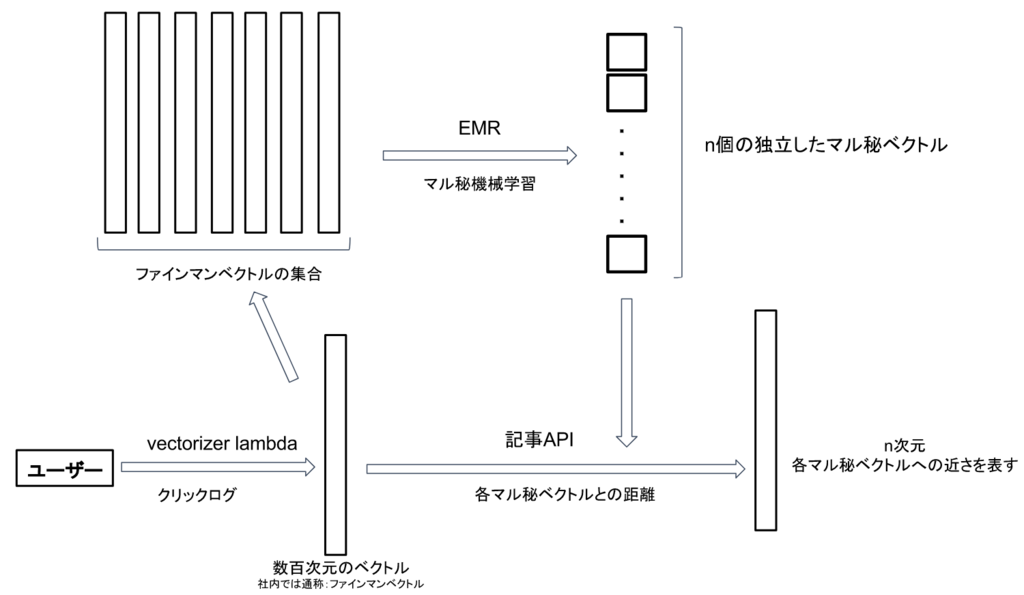
1. ユーザーはクリックするたびに社内ではファインマンベクトルと~~呼ばせている~~呼ばれているベクトルがリアルタイムに生成かつ更新される
2. 1.とは非同期に、ある時点でのファインマンベクトルを大量に用いて、Sparkで実装されたマル秘機械学習アルゴリズムでn個のマル秘ベクトルを生成する
3. 記事APIは、ユーザーがリクエストしたタイミングのそのユーザーのファインマンベクトルと、2.で生成されたｎ個のマル秘ベクトルとの距離(みたいなもの)を計算

と言った感じです。ここで出来上がるユーザーの特徴量を $w^u \in \mathbb{R}^n$ としておきます。

次に線形モデルに入力される記事の特徴量についてです。ファインマンベクトルの生成方法とマル秘機械学習アルゴリズムのおかげで、記事に関しても n個のマル秘ベクトルとの"近さ"を複数の尺度( $=:m$ )で測る事が出来ます。

つまり、複数のｎ次元ベクトル $\{ w^a_i \}_{i=1}^m \subset \mathbb{R}^n$ を生成することができます。

これらを用いてスコア計算モデル $s_t$ を

$s_t(u, a) := {\rm TimeDecay }(t,a) \times \left( \displaystyle \sum_{i=1}^m \alpha_i \times \left< w^u, w^a_i \right> \right) , \ \ t : リクエスト時間$

として設計します。このモデルは全てベクトルの内積と和の操作で完結するため、非常に高速に計算することが出来ます。

ここで ${\rm TimeDecay(t,a) }$ は時間減衰関数(time decay function)と呼ばれるユーザーからのリクエスト時間とニュース記事の情報を引数とした関数で、「基本的には時間が経つほど値が小さくなる関数」となっています。

例えば時間減衰関数に関しては次の記事が参考になります:

www.elastic.co

また、 $\alpha_1, \dots, \alpha_n$ はハイパーパラメータと呼ばれ、各独立したスコア $\left< w^u, w^a_i \right>$ を最終的なスコアにどの程度寄与させるかの重みです。

このハイパーパラメータを上手く調整することで全く気色の異なった記事リストをレスポンスしたりすることが出来ます。

もちろん各種教師あり学習アルゴリズムを用いて最適化することも出来ますが、問題設定上限られた目的関数しか設定できないため最善とは言えません。

そこで私達はこのハイパーパラメータのチューニング問題をSimulation Optimization問題として定式化して最適化するタスクを実行することにしました:

§5. Simulation Optimizationによるハイパーパラメータ最適化

システムのハイパーパラメータを柔軟なKPIに関して最適化したい場合どうすれば良いのでしょうか。例えばユーザーの滞在時間に関して最適化したい場合、パラメータと滞在時間の関係が明示的に与えることが不可能なため勾配法などを使って最適化することができません。このように入力と出力の関係が不明なまま最適化を行う問題をBlackBox関数の最適化問題と呼びます。

BlackBox関数の最適化問題は
1. 出力が確率的に揺らがない場合
2. 出力が確率的に揺らぐ場合

の２つに分類することができます。確率的に揺らがないとは、入力に関して出力が一意的に決まるという意味です。1. はDerivative Free Optimizationと呼ばれる分野で、2. はSimulation Optimizationと呼ばれる分野で今なお盛んに研究されています。

今回私達が設計したKPIは確率的なゆらぎを持っており、Simulation Optimizationに属する問題設定でした。

記事APIからのログの工夫
記事APIの実装とハイパーパラメータの分離

を行うことでSimulationOptimizationのとあるアルゴリズムとその結果をスムーズに反映することが可能となりました。

SimulationOptimizationについて詳細は後日データ分析ブログで別途解説しますが、気になる方は次のサーベイ論文を読むことをおすすめします:
[1706.08591] Simulation optimization: A review of algorithms and applications

§6. パーソナライズされた記事APIの処理

最後になりますが、ちょっとしたコード付きで記事APIの処理フローについてざっくり解説します。

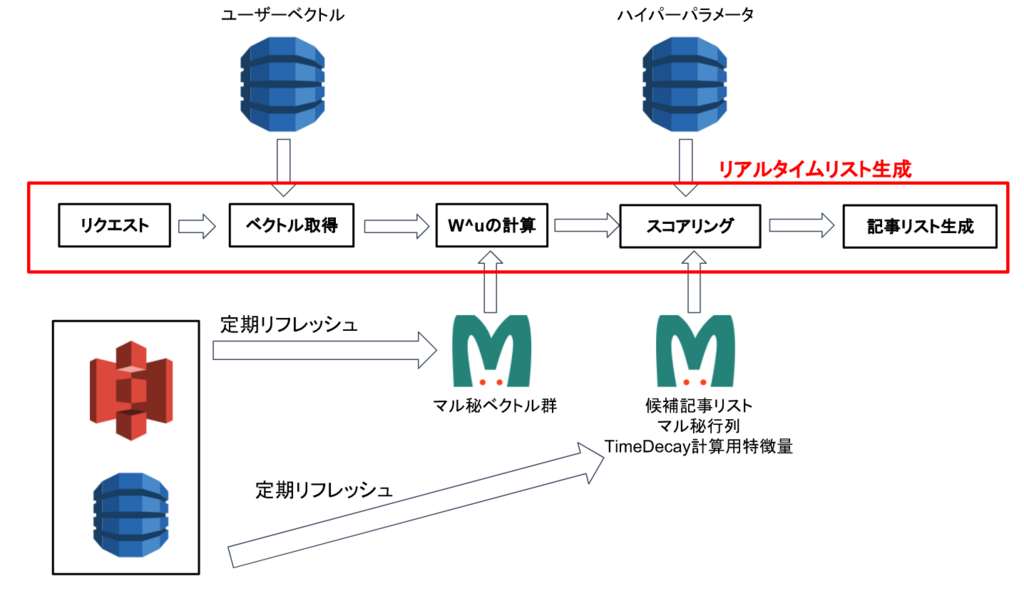
0. 時刻 $t$ にリクエストを受ける
1. DynamoDBにユーザーベクトルを取りに行く
2. $w^u \in \mathbb{R}^n$ を計算する
3. 候補記事全てに対して $s_t(w^u, a)$ を計算する ( $w^a_iは事前計算しておく$ )
4. 候補記事をスコアでソートし、上位数件をレスポンスする

といった処理フローになっています。例えば3.の部分は次のようなコードになっています:

import "gonum.org/v1/gonum/mat"

// aNum := 候補記事数
Score1 := mat.NewDense(aNum, 1, nil)
Score2 := mat.NewDense(aNum, 1, nil)
res := mat.NewDense(aNum, 1, nil)

/*
aFeature1 := article数 x n の行列. 
aFeature2 := articles数 x n の行列.
 */

// 内積処理 <w^a_i,  w^u> に相当 
Score1 = Score1.Mul(aFeature1, Wu)
Score2 = Score2.Mul(aFeature2, Wu)

// ハイパーパラメータによるスケーリング
Score1.Scale(alpha1, Score1)
Score2.Scale(alpha1, Score2)

// 和を取る(= Σの部分)
res.Add(res, Score1)
res.Add(res, Score2)